The Maths of The Code -- Part 2/2

We continue from part 1...

We doubt the laptop is turned on.

The question I wanted to answer - the question that first occurred to me after watching the show, is are you in a better position after getting one question if you pick a number or miss? Hitting a number is presented by Allwright as an always-good option, but in the first round, hitting a number immediately promotes you to a harder level. On the flipside, it decreases your likely game length, but not by much. There are intuitive reasons why it might be good or not good for your game to hit a number straight away, and no (apparent) way to compare the forces against each other.

I think this question is a great advert for "using maths", because it's immediately very not obvious what the answer is. It's even less obvious that it would change depending on the situation, but that turns out to be the case. Moreover, once we have the answer, we can (broadly speaking) make sense of it.

Anyway, onto the action. A game of The Code lasts between 3 and 10 sets. The average game is 8.25 sets, but more than half of games last 9 or 10 sets. 30% of games go to the last number - this makes sense because one number has to be the last picked, and 3/10 of the numbers need to be picked.

Oh, a quick note about combinations. There are 8*9*10 combinations for the code (no repeated digits) - but no-one cares about the order, so we divide by the 6 orders for each combination to get 120 essentially different combinations.

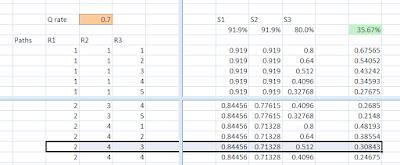
I'm going to talk a bit about paths, the routes though the 3 rounds that a game might take. I'll denote a path by 3 numbers, representing the time spent on each level.

For example, the path (1,1,1) means acing the game - picking the right numbers on your first 3 guesses. A more 'typical' path might be something like (2,4,3), answering 2 questions on the first level, 4 on the second, and 3 on the last.

(Perhaps surprisingly), there are 120 paths through the game, all equally likely. To best see this, you think about your favourite order of the 10 digits. (Say, 1234567890). Then each of the 120 equally likely possible code combinations gives a different path through the game. (Convince yourself of this if it seems unobvious).

Quite quickly, then, we can find the contestants' chances of winning the game if they are fated to a certain path - we use the chances of them surviving each set from part 1, and for the path (a,b,c) and question rate p, the chance of a win is given:

To give an example, if you know 70% of all questions, then your chances of winning the game if you were to immediately find 3 numbers:

is 67.5%. If you were destined to the path (2,4,3) which we mentioned earlier...

your chance of a win is 30.8%. 

Next to find the overall probability of winning at the start of the game. To do this we blur our condition on the path the contestants are fated to, and since each path is equally likely, it's just like taking an average.

Of course, remembering from last time that R1=R2.

Unfortunately, the distribution of the possible paths isn't symmetric like it would be if the 3 rounds were independent: a long round 1 likely means a short round 2 and 3. This means we can't really cancel the above into anything more comprehensible. In particular, we can't break down this formula to get the odds of surviving each round, which will be a shame later.

We can still put numbers into it, though, and let's set up a few examples. Suppose Clever Campbell, Borderline Brogan, and Hopeless Hayden all line up to play the Code. Campbell knows the answer to 90% of Lesley-Anne's questions, Brogan 70%, and Hayden just 40%.

At the start of the game, we give Campbell a strong 79% chance to open the safe, Brogan a fighting 36%, and Hayden a mere 5%.

All very good. We're now ready to address the question that inspired this article - what happens after 1 question?

What's now nice is that because of the uniformity of all the paths, if we just want to look at some of the paths, say - the paths of form (1,x,y) that start with getting a number correct - we can just take an average over those paths that meet the condition. That gives us the odds of success for a contestant who is destined to get a number on their first guess. [We divide out by the odds of surviving a round 1 set because we want to model the scenario that the contestant has got to the point of finding that first number.]

We do this and get the following distribution, for the chance of winning when you have got one number on the first guess.

Notice Brogan and Hayden have a better chance now - they've survived one round and are closer to the end of the game. What's remarkable is that Campbell's winning chance has now gone down, not (just) relative to if they'd guessed a wrong number, but relative to their position at the start. We'll explore the reason for this a little later.

For now, let's compare to if the contestants survive one set, but then guess their first number wrong. In this case we just calculate the opposite - the average win probability along all the other paths, and again divide out for the fact the contestants survived one round. Doing so, we find...

every player is in a better position than they were at the start - this makes sense, they're all facing the same game only with one of the incorrect numbers removed. What's interesting is that comparing the guessed correctly and guessed incorrectly scenarios, strong players like Campbell are better off having misguessed, whereas weak players like Hayden aren't. In the middle players like Brogan are mostly indifferent to the result of their first guess.

To try to make sense of this, it sometimes helps to consider the most extreme cases.

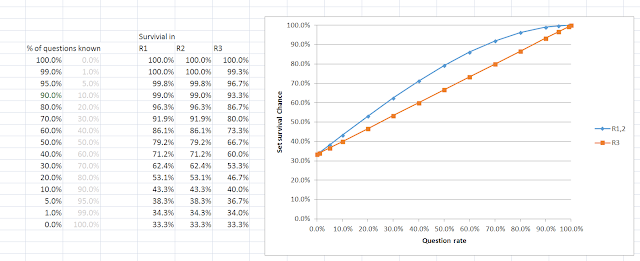
Recall this table from last time, the one telling us about the relative chances in a R1/R2 and a R3 for different player rates. Notice for a super bad player, the chances all approach 33% - they're almost totally reliant on luck - and so R1 and R3 don't look so different. It makes sense that for them, the better chance comes when the game is likely shorter.

For a super good player the R1 and R3 numbers don't look too different either - but with numbers this close to 100% we need to be looking at the chance of failure. For a 99% player, the chance of failing on R3 is around 66 times that of failing in R1, even for Campbell, the ratio is about 6.9 times as much. This makes R3 wildly more important for a good player.

(The reason for this last - to fail on R1/R2, the player needs to miss at least 2 questions - know any 2/3 and you're certain to answer correctly. But in R3 the player, 2/3 times can fail having missed only one question. When the chance of missing a question is small, then the chance of missing 1 is much larger the chance of missing 2 in a set of 3.)

Accepting that finding the first number first does give a nudge toward shorter games, and missing it a nudge toward a shorter round 3, and thinking about the extreme cases, it's hopefully possible to accept this surprising result is intuitive.

Here's a demonstration of something else that might be intuitive: guessing the first number correctly increases the likely length of R3,

and decreases the likely length of the game...

This was intuitive from some angles, but it's worth checking. We want to be sure the 'later rounds get longer' effect from getting the first guess correct doesn't outweigh the 'you're closer to the end now' effect.

In mathematical terms, we (sadly) haven't done any coupling here, we've just arranged the distributa side by side. What's apparent is the intuitive idea that compared to a miss, a hit gives you a longer likely R3, and a shorter likely game.

Hopefully, the reader is now in agreement that clever contestants want to miss on guess number 1, and less clever contestants don't. But where is the border? Unfortunately, there's not a much better answer to this than 'where we calculate it to be' - which turns out to be at a question rate of about 67.9%.

One very crude way we can try to estimate the border is looking at averages. When you hit a number on the first guess, your R2 and R3 have an average length of 3.33 sets (and R1 obviously 1), when you miss the average is 3.5 sets for R1, and 2.5 for each of R2 and R3. So (number of quotes is for effect here) """"on average"""", getting a hit on guess 1 reduces your (R1+R2) by 1.67 sets, and increases R3 by 0.83 sets.

If we plot

as a function of the rate, we should see values above one (denoting an increase in chance of winning) for low question rates and vice versa for high rates, with the curve hitting 1 around our borderline.

It should be noted before I remark that this estimate isn't very accurate, that this estimating technique is extremely roundabout. We're ignoring the fact that the round lengths are not independent variables: when one is low the others are more likely to be high. We're also ignoring the fact that the these distributions are being modified in a more complicated way than just a simple "plus 0.8333".

The plot goes like:

This estimate puts the borderline just above 58% - a fair way out, but correct in the sense of "it's in the middle". At this point I have no more elegant arguments to make - the exact value of (about) 67.9% can be found in the ways outlined earlier. That being said, I have a few more cool facts about the code (but which I'm not going to explain) that I've found using similar calculations. 

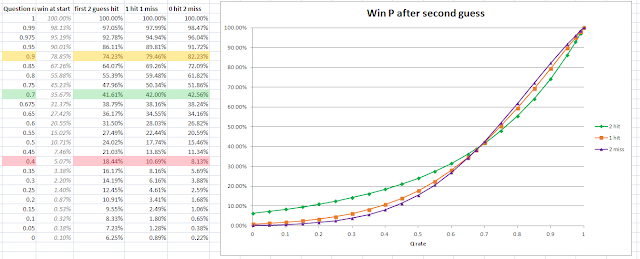
Impressively, clever players are better off if they miss on their first 2 guesses. Less good players are (unsurprisingly) better off if they get 2/2 on their first 2 guesses. It looked at first like the cut-off point might have been the same 67.9%, but a closer analysis showed:

it was around 68.5%. Also, curiously, there is a very small margin of skill in which getting 1 hit from the first 2 guesses is worse for the player than either getting 0 or 2 hits.

What about after 3 guesses? Well, unsurprisingly, the best result for all players is to get all 3 hits in their first 3 guesses. After that, though? Here's another graph. 

It's worth noting that having 1 digit after 3 guesses and having 0 digits are nearly indistinguishable. Having 2 digits, though, makes quite a difference and in accordance with the pattern already established, it's bad news for clever players and good news for the less clever.

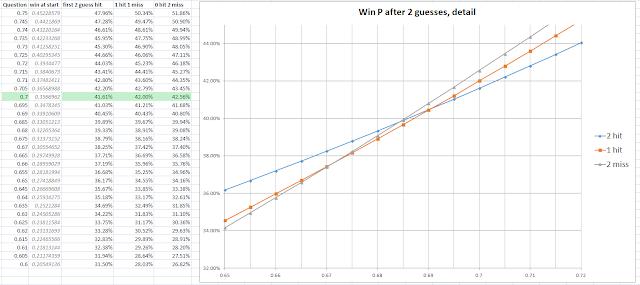
For completeness we include the detail graph for the 3 guesses situation. This time the cutoff is around 67.5%: different again, but not particularly different.

Some closing thoughts then: from observing episodes, we think most contestants on The Code will generally fall into the "below ~68%" bracket: Matt is right to be jubilant when the contestants find a number. That said, I think some of the best contestants will fall into the "above ~68%" bracket. If you appear on a future edition of The Code, you are justified in viewing Matt's excitement when your fist digit goes green as an insult to your knowledge.

We noted at the beginning of part 1 that we assumed the question difficulty was constant. Since writing that, it has been stated to not be the case. We think that if the question difficulty increases with the round, the "good to miss" effect will be even more noticeable than we have calculated, conversely if the question difficulty increases with the number of sets faced this effect should be less true than we calculated.